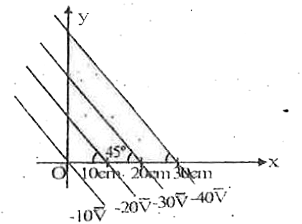
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- The gravitational field strength vecE and gravitational potential V ar...
Text Solution
|
- The gravitational field in a region is given by vecE=-(20Nkg^(-1))(hat...
Text Solution
|
- We know that electric field (E ) at any point in space can be calculat...
Text Solution
|
- We know that electric field (E ) at any point in space can be calculat...
Text Solution
|
- We know that electric field (E ) at any point in space can be calculat...
Text Solution
|
- (a) If gravitational field is given by vecE=-2xhati-3y^(2)hatj . If gr...
Text Solution
|
- The gravitational field strength vecE and gravitational potential V ar...
Text Solution
|
- The gravitational field strength vecE and gravitational potential V ar...
Text Solution
|
- The gravitational field strength vecE and gravitational potential V ar...
Text Solution
|