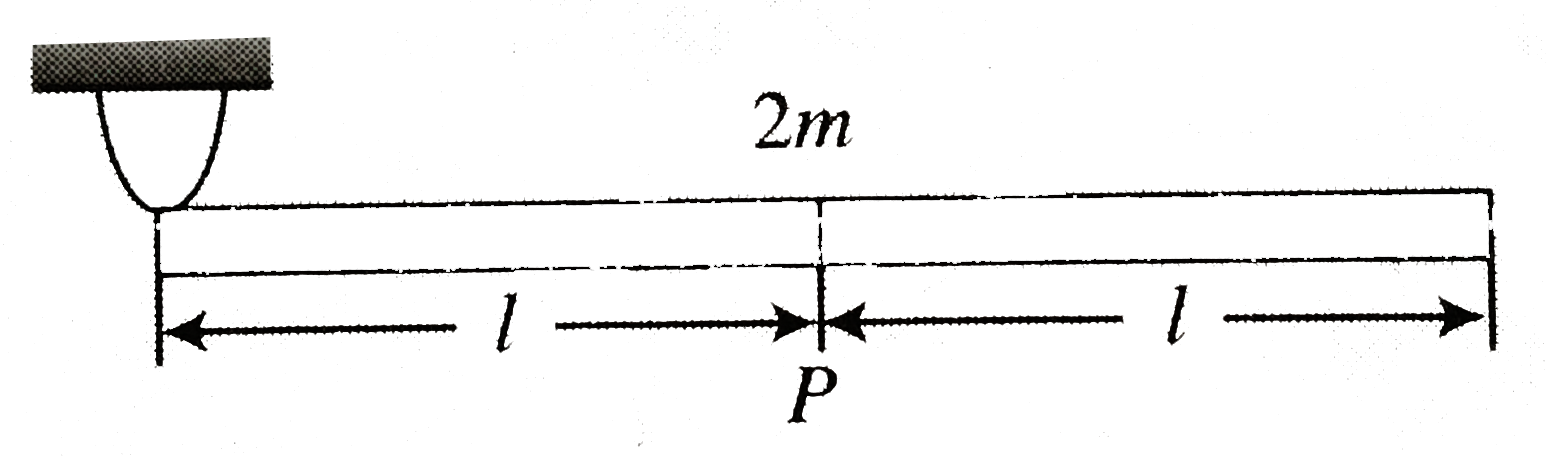Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A composite rod of mass 2m and length 2l comprises two indentica rods ...
Text Solution
|
- A composite rod of mass 2m and length 2l comprises two indentica rods ...
Text Solution
|
- A rod PQ of mass M and length L is hinged at end P . The rod is kept h...
Text Solution
|
- A rod of mass m and length l is himged about one of its ends. The rod ...
Text Solution
|
- In the figure shown, the spring are connected to the rod at one end an...
Text Solution
|
- A uniform rod of mass M and length L is hinged at its end. The rod is ...
Text Solution
|
- A rod of mass m and length l is hinged at 'its' end and released from ...
Text Solution
|
- A slender rod is hinged at its top end and hanging freely in a vertica...
Text Solution
|
- One end of a uniform rod of length l and mass m is hinged at A. It is ...
Text Solution
|