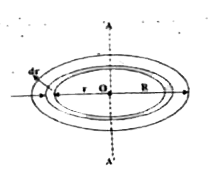
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- The M.I. of a ring of mass radius R about the axis passing through the...
Text Solution
|
- Calculate the M.I. of a thin uniforn ring about an axis tangent to the...
Text Solution
|
- Calculate the M.I. of a thin uniform ring about an axis tangent to the...
Text Solution
|
- The M.I. of a ring about an axis passing through its centre and perpen...
Text Solution
|
- The M.I. of a thin ring of mass M and radius R about an axis through t...
Text Solution
|
- A disc of radius r is removed from the centre of a disc of mass M and ...
Text Solution
|
- Moment of inertia of a circular ring of mass m and radius r about the ...
Text Solution
|
- Radius of gyration of a ring of radius R about an axis passing through...
Text Solution
|
- A disc of mass .m. and radius R has a concentric hole of radius .r.. I...
Text Solution
|