Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
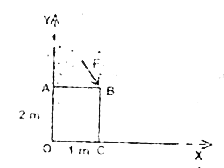
- A rectangular plate in the x-y plane is shown in the figure. A force b...
Text Solution
|
- A force F=-K(yhati+xhatj) (where K is a positive constant) acts on a p...
Text Solution
|
- If bar(a)=hat(i)+2hat(j),b=-2hat(i)+hat(j),bar(c)=4hat(i)+3hat(j) find...
Text Solution
|
- If bar(a)=3hat(i)-hat(j)+4hat(k)," "bar(b)=2hat(i)+3hat(j)-hat(k)," "b...
Text Solution
|
- A force F=-K(yhati+xhatj) (where K is a positive constant) acts on a p...
Text Solution
|
- यदि bar(a) = 2hat(i) - hat(j) + hat(k ), bar(b) = hat(i) + 2hat(j) - h...
Text Solution
|
- यदि bar(a) = 5hat(i) + 3hat(j) + 2hat(k) + 2hat(k) , bar(b) = - 2hat(i...
Text Solution
|
- A force vec(F) = (2 hat(i) + 3 hat(j) + 4 hat(k)) N is applied to a po...
Text Solution
|
- Given two vectors ,bar(A)=hat i-2hat j-3hat k and bar(B)=4hat i-2hat j...
Text Solution
|