Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
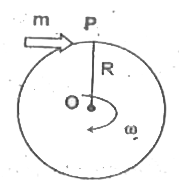
- A bullet of mass m collides inelastically at the periphery of a disc o...
Text Solution
|
- A uniform disc of mass m and radius R rotates about a fixed vertical a...
Text Solution
|
- A man of mass m stands on a horizontal platform in the shape of a disc...
Text Solution
|
- A uniform disc of mass m and radius R rotates about a fixed vertical a...
Text Solution
|
- A disc of mass m and radius R lies flat on a smooth horizontal table. ...
Text Solution
|
- A particle of mass m strikes elastically with a disc of radius R, with...
Text Solution
|
- A point mass m collides with a disc of mass m and radius R resting on ...
Text Solution
|
- A uniform disc of mass M and radius R is rotating in a horizontal plan...
Text Solution
|
- A disc of mass M and radius R is rolling with angular speed w on horiz...
Text Solution
|