Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
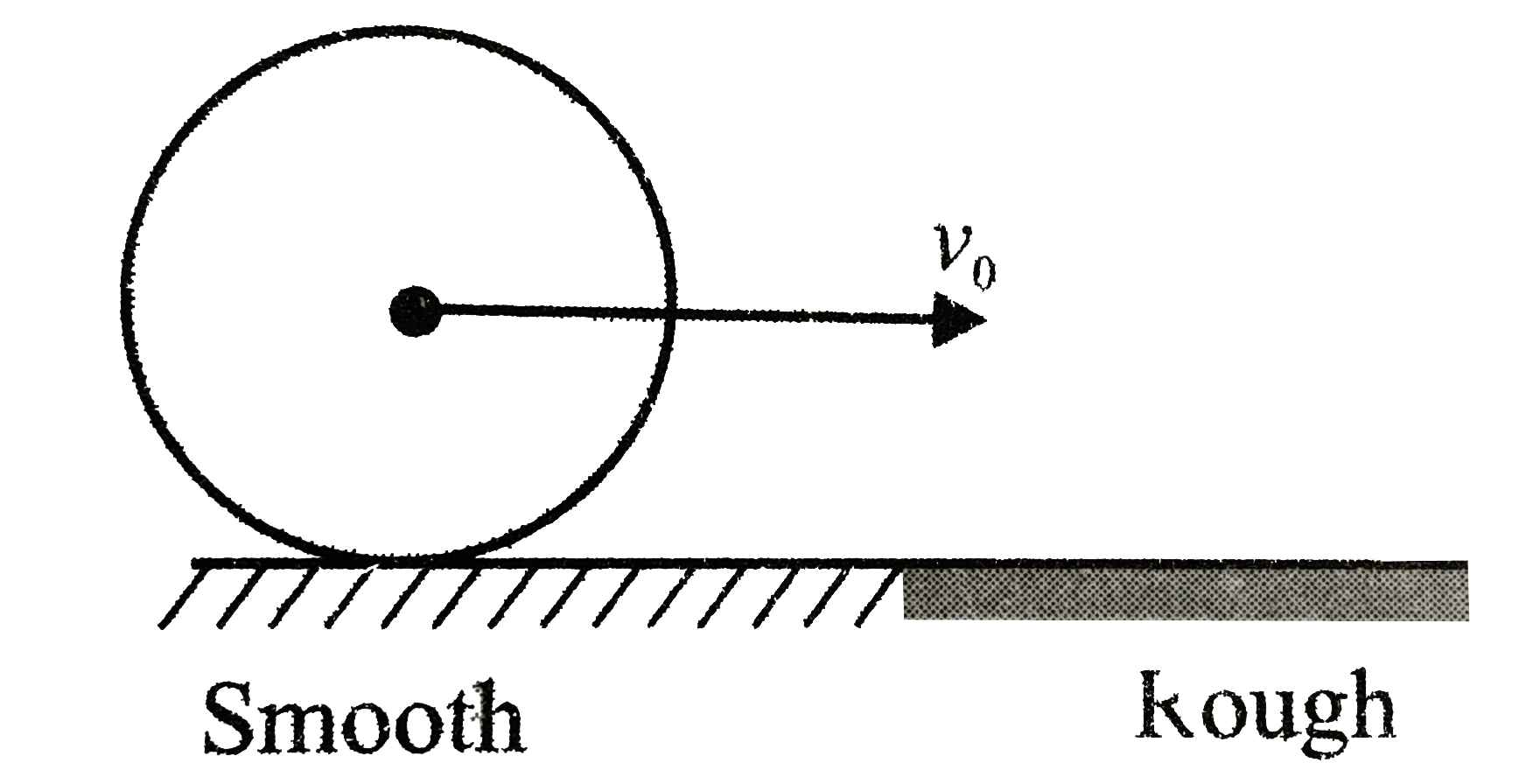
- A sphere moving with a velocity v(0) on a smooth surface suddenly ente...
Text Solution
|
- Assertion: A solid sphere and a hollow sphere are rolling on ground wi...
Text Solution
|
- A sphere moving with a velocity v(0) on a smooth surface suddenly ente...
Text Solution
|
- A sphere rolling on a horizontal rough surface Collides elastically wi...
Text Solution
|
- A solid sphere of mass m and radius R rolls without slipping on the ho...
Text Solution
|
- A hollow sphere is rolling without slipping on a rough surface. The ra...
Text Solution
|
- A solid sphere is moving on a horizontal plane. Ratio of its translati...
Text Solution
|
- A sphere is rolling on a horizontal surface without slipping. The rati...
Text Solution
|
- A sphere moving with a speed v(0) on a smooth surface suddenly enters ...
Text Solution
|