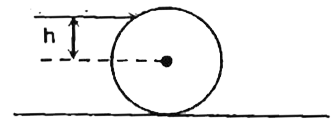
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- In order to get a billiard ball to roll without sliding from the start...
Text Solution
|
- A solid sphere of mass M and radius R is hit by a cue at a height h ab...
Text Solution
|
- A uniform ball of radius r rolls without slipping down from the top of...
Text Solution
|
- The cue stick hits a cue ball horizontally a distance x above the cent...
Text Solution
|
- A billiard ball is struck by a cue when it starts moving with velocity...
Text Solution
|
- Show that in order to get a billiard ball to roll without sliding from...
Text Solution
|
- Where must the cue hit a billiard ball so that it rolls without slidin...
Text Solution
|
- A sphere of radius r is rolling without sliding. What is ratio of rota...
Text Solution
|
- A small solid sphere rolls without slipping along the track shown in f...
Text Solution
|