Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
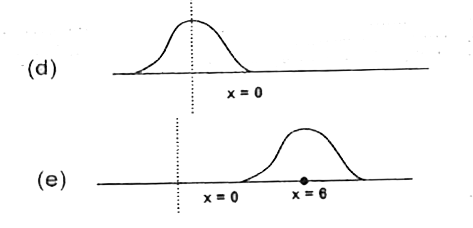
- A wave is propagating on a long stretched string along its length take...
Text Solution
|
- A wave is propgting of a long stretched string along its length taken ...
Text Solution
|
- The displacement of the particle at x = 0 of a stretched string carryi...
Text Solution
|
- A wave propagates on a string in the positive x-direction at a velocit...
Text Solution
|
- The equation of a wave travelling on a string stretched along the X-ax...
Text Solution
|
- A wave is propagating along the length of a string taken as positive x...
Text Solution
|
- एक लंबी तनी हुई डोरी पर एक तरंग धनात्मक -दिशा में चल रही है । इसका समी...
Text Solution
|
- A wave is propagating on a long stretched string along its length take...
Text Solution
|
- A wave is propagating on a long stretched string along its length take...
Text Solution
|