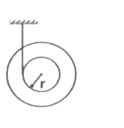
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A YO-YO of mass M and moment of inertia I about its c.m. is having a s...
Text Solution
|
- Figure shows three identical yo-yos initially at rest on a horizontal ...
Text Solution
|
- A yo-yo, arranged as shown, rests on a frictionless surface. When a fo...
Text Solution
|
- A yo-yo is released from your hand with the string wrapped around your...
Text Solution
|
- A yo-yo is resting on a perfectly rough horizontal table. Forces F(1),...
Text Solution
|
- A yo-yo is placed on a rough horizontal surface and a constant force F...
Text Solution
|
- A Yo-Yo of mass m has an axle of radius b and a spool of radius R. The...
Text Solution
|
- Figure shows a yo-yo placed on a rough surface friction is sufficient ...
Text Solution
|
- A yo-yo is resting on a perfectly rough horizontal table . Forces F(1)...
Text Solution
|