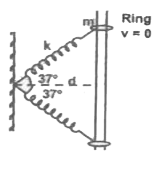
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- One end a light spring of natural length d and spring constant k ( = m...
Text Solution
|
- A ring of mass m is attached to a horizontal spring of spring constant...
Text Solution
|
- A Bead of mass m is attached to one end of a spring of natural length ...
Text Solution
|
- A ring of mass m can slide over a smooth vertical rod. The ring is con...
Text Solution
|
- One end of a light spring of natural length 4m and spring constant 170...
Text Solution
|
- स्प्रिंग नियताकं k तथा स्वाभाविक लंबाई h वाले एक स्प्रिंग का एक सिरा...
Text Solution
|
- One end of a light spring of natural length d and spring constant k is...
Text Solution
|
- A mass m is attached to the free end of a massless spring of spring co...
Text Solution
|
- one end of a spring of natural length ha and spring constant k is fixe...
Text Solution
|