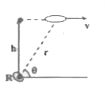
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A jet plane flying at a constant velocity v at a height h = 8 km is be...
Text Solution
|
- The angle of elevation of a jet plane from a point A on the grund is 6...
Text Solution
|
- The angle of elevation of a jet plane from a point A on the ground is ...
Text Solution
|
- The angle of elevation of a jet plane from a point A on the grou...
Text Solution
|
- A jet plane is flying horizontally with a velocity 600 km h^(-1). The ...
Text Solution
|
- जमीन पर एक बिंदु A से एक जेट फाइटर का उन्नयन कोण 60^(@) है|10 सेकंड क...
Text Solution
|
- जमीन पर एक बिंदु A से एक जेट - फाइटर का उन्नयन कोण 60^(@) है। 15 ...
Text Solution
|
- जमीन पर के किसी बिंदु से एक जेट - फाइटर का उन्नमन कोण 60^(@) है ।...
Text Solution
|
- भूमि के किसी बिंदु से एक जेट विमान का उन्नयन कोण 60^@ है । 20 सेकंड क...
Text Solution
|