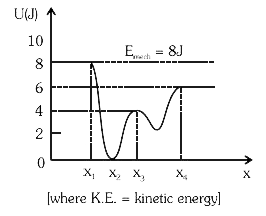A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Given below is the plot of a potential energy function U(x) for a syst...
Text Solution
|
- A single conservative force F(x) acts on a 1.0-kg particle that moves ...
Text Solution
|
- A single conservative force F(x) acts on a 1.0-kg particle that moves ...
Text Solution
|
- If x,F and U denote the dispalcement, force acting on and potential en...
Text Solution
|
- As a particle moves along the x- axis, it is acted upon by a conservat...
Text Solution
|
- A single conservative force F(x) acts on a particle that moves along t...
Text Solution
|
- If x, F and U denote the displacement force acting on and potential en...
Text Solution
|
- A single conservative force F(x) acts on particle that moves along the...
Text Solution
|
- The potential energy of a particle under a conservative force is given...
Text Solution
|