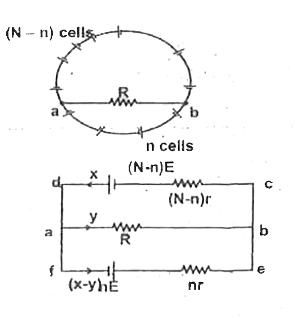
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- n' cells , each of emf 'e' and internal resistance 'r' are connected i...
Text Solution
|
- There are n cells, each of emf E and internal resistance r, connected ...
Text Solution
|
- Four cells, each of emf E and internal resistance r, are connected in ...
Text Solution
|
- In a circuit a cell with internal resistance r is connected to an exte...
Text Solution
|
- A cell of emf epsilon and internal resistance (r) is connected in seri...
Text Solution
|
- Four cells each of emf E are internal resistance r, are connected In s...
Text Solution
|
- A cell of emf E and internal resistance r is connected to a variable e...
Text Solution
|
- A cell of emf 10 V and internal resistance 3 Omega is connected in par...
Text Solution
|
- A cell of emf E and internal resistance r is connected in series with ...
Text Solution
|