Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
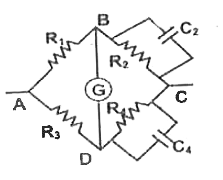
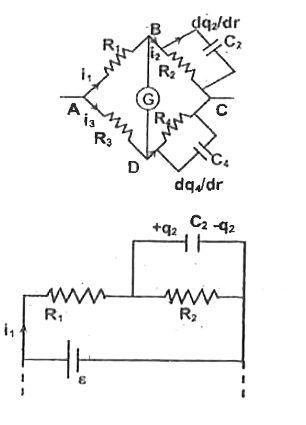
- Consider a Wheatstone bridge with resistance and capacitance connected...
Text Solution
|
- In a Wheatstone bridge resistance connected the bridge is balanced , w...
Text Solution
|
- Four resistances of 16 Omega , 12 Omega , 4 Omega and 9 Omega respecti...
Text Solution
|
- यदि सन्तुलित व्हीटस्टोन ब्रिज की प्रत्येक भुजा तथा धारामापी का प्रतिरो...
Text Solution
|
- In Wheatstone bridge, the resistances in four arms are 10Omega,10Omega...
Text Solution
|
- Statement I : If the resistance of the first two arms P and Q of a bal...
Text Solution
|
- व्हीटस्टोन सेतु की भुजाओं में प्रतिरोध चित्र में दर्शाए गए अनुसार लगे ...
Text Solution
|
- व्हीटस्टोन ब्रिज की भुजाओं में प्रतिरोध चित्र में दिखाये अनुसार लगा रख...
Text Solution
|
- Tricks for Combination Of Resistance,WheatStone Bridge
Text Solution
|