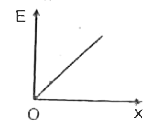
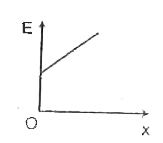
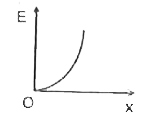
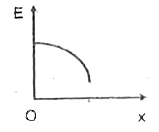
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A cylindrical conductor has uniform cross-section. Resistivity of its ...
Text Solution
|
- A conductor of length l has a non-uniform cross-section. The radius of...
Text Solution
|
- A rod is made of uniform material and has non-uniform cross section. I...
Text Solution
|
- A conductor of resistivity rho and resistance R, as shown in the figur...
Text Solution
|
- Current flows through a straight cylindrical conductor of radius r. Th...
Text Solution
|
- Two cylindrical conductors with equal cross-sections and different res...
Text Solution
|
- A cylindrical conductor has length l and area of cross section A. Its ...
Text Solution
|
- Assertion: The resistance of a conductor decreases with increase in cr...
Text Solution
|
- A rod of length L is of non uniform cross-section. Its mass per unit l...
Text Solution
|