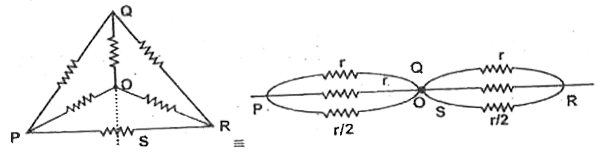
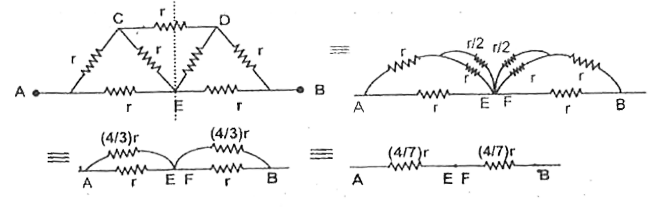
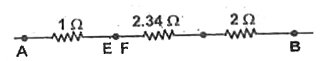Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- It is desired to make a 20Omega coil of wire, which has a zero thermal...
Text Solution
|
- It is desired to make a 20Omega coil of wire, which has a zero thermal...
Text Solution
|
- It is desired to make a 20.0Omega coil of wire whose temperature coeff...
Text Solution
|
- Two resistances R1 and R2 are made of different materials. The tempera...
Text Solution
|
- For two resistors R1 and R2 , connected in parallel, find the relative...
Text Solution
|
- यदि समांतरक्रम में जुड़े दो प्रतिरोध के प्रतिरोध R1 और R2 हों, तो उनका...
Text Solution
|
- Prove it R= R1 + R2 Where R is the resistors connected in series R1 An...
Text Solution
|
- दो प्रतिरोध R(1) और R(2) भिन्न पदार्थो के बने हुए है । R(1)के पदार्...
Text Solution
|
- An aluminium ( alpha(Al) = 4 xx 10^(-3) //""^(0) C) wire resistance R1...
Text Solution
|