To solve the problem of determining the variation of potential energy (U) as a fifth charge is moved along the X-axis in the presence of four identical charges located at the vertices of a square in the YZ plane, we can follow these steps:
### Step-by-Step Solution:
1. **Understanding the Configuration**:
- We have four identical charges, each denoted as \( Q \), placed at the vertices of a square in the YZ plane.
- The square has a side length \( a \), and the coordinates of the charges can be represented as:
- \( (0, \frac{a}{2}, \frac{a}{2}) \)
- \( (0, \frac{a}{2}, -\frac{a}{2}) \)
- \( (0, -\frac{a}{2}, \frac{a}{2}) \)
- \( (0, -\frac{a}{2}, -\frac{a}{2}) \)
2. **Position of the Fifth Charge**:
- The fifth charge, denoted as \( q \), is moved along the X-axis. Its position can be represented as \( (x, 0, 0) \).
3. **Calculating the Distance**:
- The distance \( d \) from the fifth charge to any of the four charges can be calculated using the distance formula. For a charge located at \( (0, \frac{a}{2}, \frac{a}{2}) \), the distance \( d \) is:
\[
d = \sqrt{x^2 + \left(\frac{a}{2}\right)^2 + \left(\frac{a}{2}\right)^2} = \sqrt{x^2 + \frac{a^2}{2}}
\]
4. **Potential Energy Calculation**:
- The potential energy \( U \) due to one charge \( Q \) at distance \( d \) is given by:
\[
U = k \frac{Qq}{d}
\]
- Since there are four identical charges, the total potential energy \( U_{total} \) when the fifth charge is at position \( x \) is:
\[
U_{total} = 4 \cdot k \frac{Qq}{d} = 4k \frac{Qq}{\sqrt{x^2 + \frac{a^2}{2}}}
\]
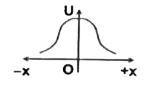
5. **Analyzing the Variation of Potential Energy**:
- As \( x \) approaches 0, \( d \) becomes \( \sqrt{\frac{a^2}{2}} \), which is the minimum distance, leading to maximum potential energy.
- As \( |x| \) increases, \( d \) increases, leading to a decrease in potential energy.
- Therefore, the potential energy \( U \) is symmetric about the origin and reaches a maximum at \( x = 0 \).
6. **Graphical Representation**:
- The graph of potential energy \( U \) versus \( x \) will show a peak at \( x = 0 \) and will decrease symmetrically as \( |x| \) increases.
### Conclusion:
The variation of potential energy \( U \) along the X-axis is represented by a curve that peaks at the origin and decreases symmetrically as you move away from the origin in either direction.