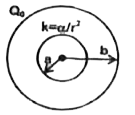
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- An ice ball of radius a and mass m is placed at 0^@C inside a thick ho...
Text Solution
|
- A hollow sphere of glas whose external and internal radii are 11 cm an...
Text Solution
|
- A metallic cylindrical vessel whose inner and outer radii are r1 and r...
Text Solution
|
- A layer of ice of thickness y is on the surface of a lake. The air is ...
Text Solution
|
- A hollow sphere of glass whose external and internal radii are 11cm an...
Text Solution
|
- On a cold winter dry, the temperature of atmosphere is -T^(@)C . The c...
Text Solution
|
- The ice is filled in a hollow glass sphere of thickness 2mm and extern...
Text Solution
|
- Latent heat of fusion / melting of ice:
Text Solution
|
- Latent heat of fusion / melting of ice:
Text Solution
|