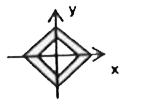
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- The gravitational field in a region is given by vecE=(yhati+ xhatj) N/...
Text Solution
|
- The gravitational field in a region is given by vecE=-(20Nkg^(-1))(hat...
Text Solution
|
- The potential field of an electric field vecE = (yhati + yhati) is
Text Solution
|
- The electric field intensity at all points in space is given by vecE =...
Text Solution
|
- An electric field vecE=(yhati+xhatj) When expressed by equations, the ...
Text Solution
|
- The gravitational field in a region is given by vecE = (4hati +3hatj)N...
Text Solution
|
- The gravitational field in a region is given by vecE = (5hati + 12hatj...
Text Solution
|
- The gravitational field in a region is giveny by vecE = (2hati +3hatj)...
Text Solution
|
- The gravitational field in a region is given by vecE =(5hati + 12hatj)...
Text Solution
|