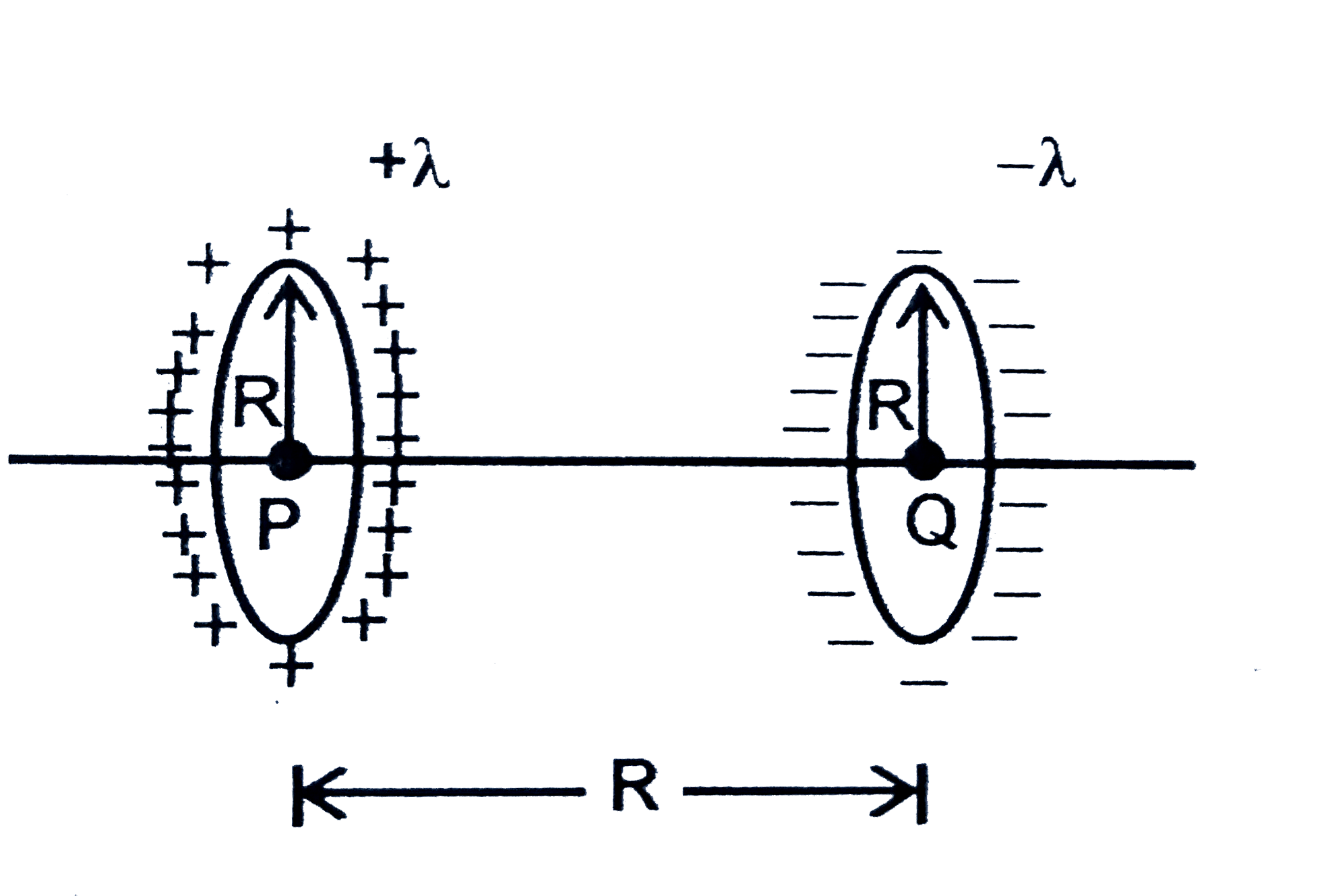
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Two fixed insulating rings A and B carry charges with uniform linear c...
Text Solution
|
- Two identical coaxial rings each of radius R are separated by a distan...
Text Solution
|
- A half ring of radius r has a linear charge density lambda.The potenti...
Text Solution
|
- A rod with linear charge density lambda is bent in the shap of circula...
Text Solution
|
- Two fixed insulating rings A and B carry ahanges with uniform linear a...
Text Solution
|
- Two semicircular rings lying in same plane, of uniform linear charge d...
Text Solution
|
- Two circular rings A and B, each of radius a = 30cm, are placed coaxia...
Text Solution
|
- Eight charges each of value q each are placed on a ring of radius R pl...
Text Solution
|
- A charge -q is placed at the axis of a charged ring of radius at a dis...
Text Solution
|