A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
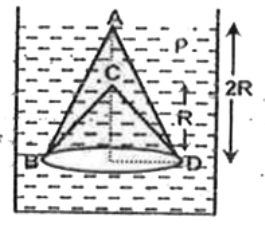
- A solid cone of uniform density and height 2R and base radius R has a ...
Text Solution
|
- A solid cone of height H and base radius H/2 floats in a liquid of den...
Text Solution
|
- A uniform solid right circular cone of base radius R is joined to a un...
Text Solution
|
- A cone of radius r and height r is under a liquid of density d.its bas...
Text Solution
|
- A frustum of a uniform solid cone has base radius R and height H as sh...
Text Solution
|
- A cone of radius R and height H , is hanging inside a liquid of densit...
Text Solution
|
- यदि r त्रिज्या वाले एक ठोस गोले को पिघलाकर इसे r ऊँचाई के ठोस शंकु के ...
Text Solution
|
- A solid sphere of radius r melted and recast into the shape of a solid...
Text Solution
|
- A solid sphere of radius r is melted and recast into the shape of a so...
Text Solution
|