Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
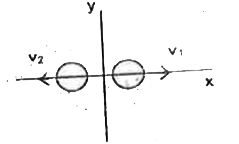
- A small ball on a frictionless horizontal surface moves towards right ...
Text Solution
|
- A ball moving with a velocity v hits a massive wall moving towards the...
Text Solution
|
- A man swims to and fro along the bank of a river with a velocity v rel...
Text Solution
|
- A ball collides with a frictionless wall with velocity u as shown in t...
Text Solution
|
- A small ball thrown at an initial velocity v(0) at an angle alpha to t...
Text Solution
|
- A small ball on a frictionless horizontal surface moves towards right ...
Text Solution
|
- एक घर्षणयुक्त क्षैतिज सतह पर रेखीय चाल v से एक ठोस गोला चल रहा है। यह ...
Text Solution
|
- A ball moving with speed v collides with a horizontal smooth surface a...
Text Solution
|
- A ball moving with a velocity v hits a massive wall moving towards the...
Text Solution
|