Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- In the figure shown, initially the spring is in relaxed position. A b...
Text Solution
|
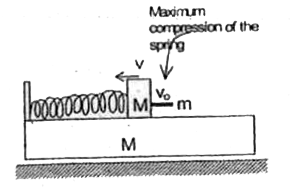
- A block of mass m is moving with an initial velocity v0 towards a stat...
Text Solution
|
- In figure, the stiffness of the spring is k and mass of the block is m...
Text Solution
|
- A block of mass m is moving with a speed v on a horizontal rough surfa...
Text Solution
|
- A block of mass m moving at a speed v0 compresses a spring of spring c...
Text Solution
|
- A block of mass 180 g is placed on a spring (spring constant k = 120 N...
Text Solution
|
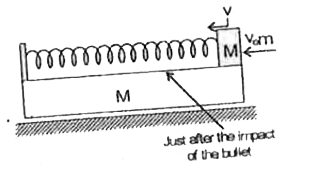
- A bullet of mass m strikes a block of mass M connected to a light spri...
Text Solution
|
- Figure. shows a rough horizontal plane which ends in a vertical wall, ...
Text Solution
|
- A block of mass m is placed on a smooth block of mass M = m with the h...
Text Solution
|