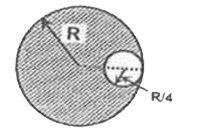
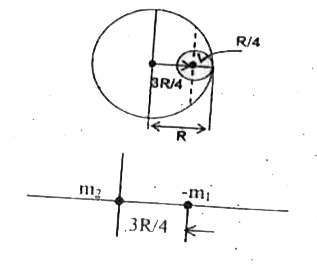
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Find the centre of mass of the shaded portion of a disc.
Text Solution
|
- Find the centre of mass of a unifrom (a) half-disc,(b) quarter-disc.
Text Solution
|
- A uniform disc of radius R=20cm has a round cut as shown in figure. Th...
Text Solution
|
- From a thin uniform disc of radius 2R. Another disc of diameter 2R is ...
Text Solution
|
- The centre of mass of the shaded portion of the disc is: ( The mass is...
Text Solution
|
- From a circular disc of radius R, a triangular portion is cut (sec fig...
Text Solution
|
- Find the area of shaded portion
Text Solution
|
- Find the area of shaded portion.
Text Solution
|
- A uniform disc of radius R has a round disc of radius R/3 cut as shown...
Text Solution
|