Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A steel ball of mass 0.5 kg is fastened to a cord 20 cm long and fixed...
Text Solution
|
- A steel ball of mass 0.5 kg is fastened to a cord 20 cm long and fixed...
Text Solution
|
- A ball of 4 kg mass moving with a speed of 3ms^(-1) has a head on elas...
Text Solution
|
- The ball is released when the string is horizontal. The collision betw...
Text Solution
|
- A steel ball weighting 1 kg is fastened to a cord 1 m long and is rele...
Text Solution
|
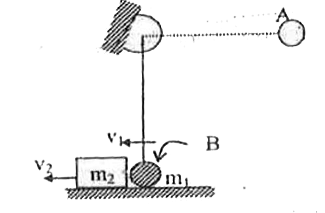
- A block of mass 5 kg resting on a horizontal surface is connected by a...
Text Solution
|
- A steel ball of mass 0.5 kg is dropped from a height of 4 m on to a ho...
Text Solution
|
- A block of mass 5 kg resting on a horizontal surface is connected by a...
Text Solution
|
- A ball of mass 4 kg moving on a smooth horizontal surface makes an ela...
Text Solution
|