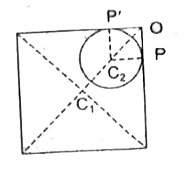
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A disc of radius R is placed on a square plate of edge 4R made up of t...
Text Solution
|
- From the circular disc of radius 4R two small discs of radius R are cu...
Text Solution
|
- A disc of radius r is cut from a larger disc of radius 4r in such a wa...
Text Solution
|
- Centre of mass of the system lies inside disc or square plate and why ...
Text Solution
|
- A square plate of edge d and a circular disc of diameter d are placed ...
Text Solution
|
- A disc of radius R is placed on a square plate of edge 4R made up of t...
Text Solution
|
- A circular disc of diameter d and a square plate of side d are placed ...
Text Solution
|
- A uniform disc of diameter R/2 is put over another uniform disc of rad...
Text Solution
|
- A circular disc of diameter d and a square plate of side d are placed ...
Text Solution
|