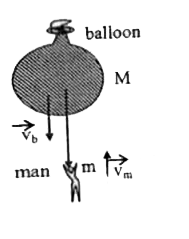
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A ball of mass 50 g is dropped from a height h = 10 m . It rebounds lo...
Text Solution
|
- A rubber ball of mass 50 g falls from a height of 5m and rebounds to a...
Text Solution
|
- A ball is dropped on the floor from a height of 10m. It rebounds to a ...
Text Solution
|
- A ball of mass 50 gm is dropped from a height h=10m. It rebounds losin...
Text Solution
|
- A ball is dropped onto the floor from a height of 10 m. It rebounds to...
Text Solution
|
- A ball of mass 1 kg is dropped from height 9.8 m, strikes with ground ...
Text Solution
|
- A rubber ball dropped from 24 m height loses its kinetic energy by 25%...
Text Solution
|
- A rubber ball of mass 100 g falls from a height of 1 m rebounds to a h...
Text Solution
|
- A ball of mass 10 gm dropped from a height of 5m hits the floor and re...
Text Solution
|