Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
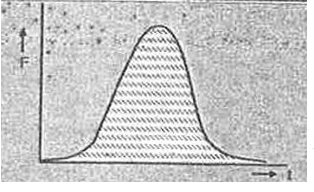
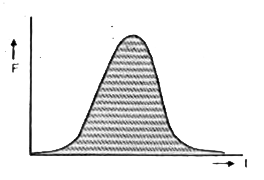
- The area of F.t curve is A. If one of the colliding bodies of mass m i...
Text Solution
|
- A body of rest mass m0 collides perfectly inelastically at a speed of ...
Text Solution
|
- Body A of mass 4m moving with speed u collides with another body B of ...
Text Solution
|
- A body of a mass m moving with speed v collides elastically head on wi...
Text Solution
|
- A body of mass 'm' moving with certain velocity collides with another ...
Text Solution
|
- A 6 kg mass collides with a body at rest. After the collision, they tr...
Text Solution
|
- The area of F-t curve is A, where 'F' is the force on one mass due to ...
Text Solution
|
- A body of mass M moving with a speed u has a ‘head on’, perfectly elas...
Text Solution
|
- A 5kg mass collides with a body at rest. After the collision, they tra...
Text Solution
|