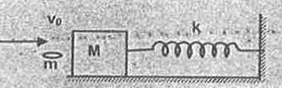
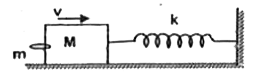
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A bullet of mass m strikes a block of mass M connected to a light spri...
Text Solution
|
- A bullet of mass m strikes a block of mass M. The bullet remains embed...
Text Solution
|
- A bullet of mass m moving with velocity v strikes a block of mass M at...
Text Solution
|
- A wooden block of mass M rests on a horizontal surface. A bullet of ma...
Text Solution
|
- A block of mass M lying on a smooth· horizontal surface is rigidly att...
Text Solution
|
- A bullet of mass m is fired into a block of wood of mass M which hangs...
Text Solution
|
- A bullted of mass m embeds itself in a block of mass M resting on a sm...
Text Solution
|
- v चाल से चलती हुई द्रव्यमान की एक गोली m द्रव्यमान के स्थिर ब्लॉक से ट...
Text Solution
|
- A bullet of mass m moving with a speed v strikes a wooden block of mas...
Text Solution
|