Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
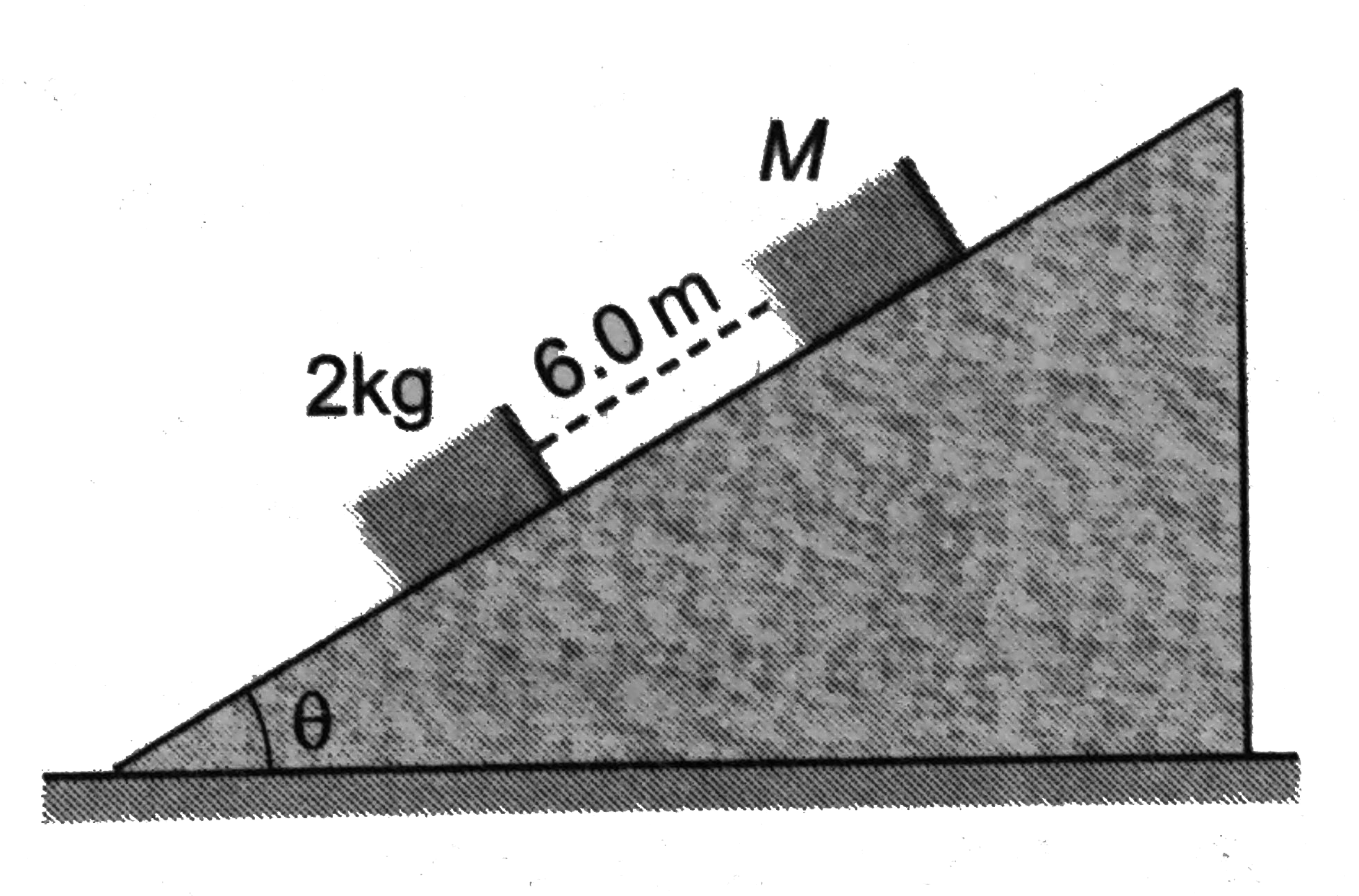
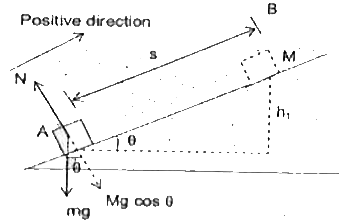
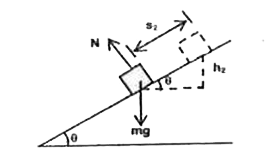
- Two blocks of masses 2kg and M are at rest on an inclined plane and ar...
Text Solution
|
- Two blocks of mass 2 kg and M are at rest as an inclined plane and ar...
Text Solution
|
- A block of mass m is placed at rest on an inclination theta to the hor...
Text Solution
|
- Two blocks of masses 2kg and M are at rest on an inclined plane and ar...
Text Solution
|
- An inclined plane is moving with Constant velocity v = 4 m//s on a hor...
Text Solution
|
- A block of mass m=2kg is resting on a rough inclined plane of inclinat...
Text Solution
|
- Block of mass 10 kg is moving on inclined plane with constant velocity...
Text Solution
|
- A block of mass m is at rest on a rough inclined plane of angle of inc...
Text Solution
|
- A block of mass M rests on an inclined plane. If the coefficient of fr...
Text Solution
|