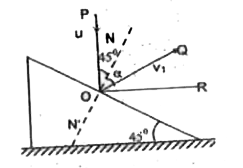
Line of impact is a straight line perpendicular to the incline. Normal reaction force between the body and the wedge acts along the impact line. This normal force becomes internal force when we consider (wedge + body) as a total system. But normal reaction is considerable in magnitude because the impact force during collision has contribution towards making of the normal force. Momentum of the system is conserved along the line perpendicular to this normal force. ....(i)
Momentum of the system is conserved along horizontal .....(ii)
Momentum of the particle is conserved along the common tangent at the point of impact. .....(iii)
As this is an elastic collision, relative velocity of separation along the impact line = Relative velocity of approach. .....(iv)
If the wedge were at rest then the particle would deflect along the horizontal after collision because it is an elastic collision .....(v)
As, in this case, wedge is moving, the object would not be deflected horizontal, but at an angle `.alpha.` to the line of impact ....(vi)
Velocity of particle before impact `u=sqrt(2gh)` along `vec(PO)`
Velocity of particle after collision `= v_(1)` along `vec(OQ)`
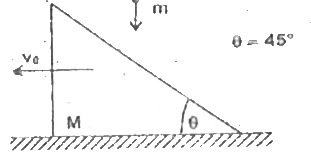
Velocity of wedge before collision `= v_(0)` along `vec(RO)`
Velocity of wedge after collision `= v_(2)` along `vec(RO)`
Velocity of approach = velocity of separation
`v_(0)cos 45^(@)-ucos 45^(@)=-v_(1)cos alpha - v_(2)cos 45^(@)`
`rArr v_(1)cos alpha + (v_(2))/(sqrt(2))=(u)/(sqrt(2))-(v_(0))/(sqrt(2))`
`sqrt(2)v_(1)cos alpha + v_(2)=u-v_(0) " " ....(A)`
Conserving momentum along the horizontal
`Mv_(0)=Mv_(2)-mv_(1)cos (45^(@)-alpha)`
`rArr 2v_(0)=2v_(2)-v_(1)cos (45^(@)-alpha)`
`rArr 2v_(2)-v_(1)cos(45^(@)-alpha)=2v_(0) " "` ....(B)
Conserving momentum along the common tangent
`mu sin 45^(@)=mv_(1)sin alpha`
`rArr v_(1)sin alpha = u " "` ....(C )
On solving (A), (B) and (C )
`v_(1)=sqrt(u^(2)[(u(4-sqrt(2))-6v_(0))/(20)]^(2))` and `v_(2)=(v_(0)+(sqrt(2)+1)u)/(5)`