Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
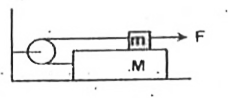
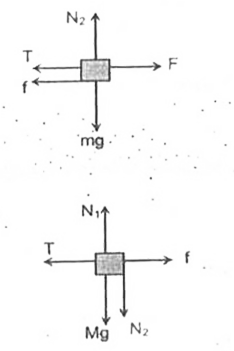
- A small block of mass 'm' is placed on a plank of mass 'M'. The block ...
Text Solution
|
- A small block of mass m is placed on a plank of masss M .The block is ...
Text Solution
|
- A block of mass M= 4 kg of height and breath b is placed on a rough pl...
Text Solution
|
- A block of mass m is placed in equilibrium on a moving plank. The maxi...
Text Solution
|
- A block of mass m=2kg of shown dimensions is placed on a plank of mass...
Text Solution
|
- In the figure shown, a solid sphere of mass 'm' and radius r is releas...
Text Solution
|
- A plank of mass 10 kg and a block of mass 2 kg are placed on a horizon...
Text Solution
|
- A block of mass'm' it kept over the smooth surface of the plank of mas...
Text Solution
|
- A block of mass m is gently placed over a massive plank moving horizon...
Text Solution
|