Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
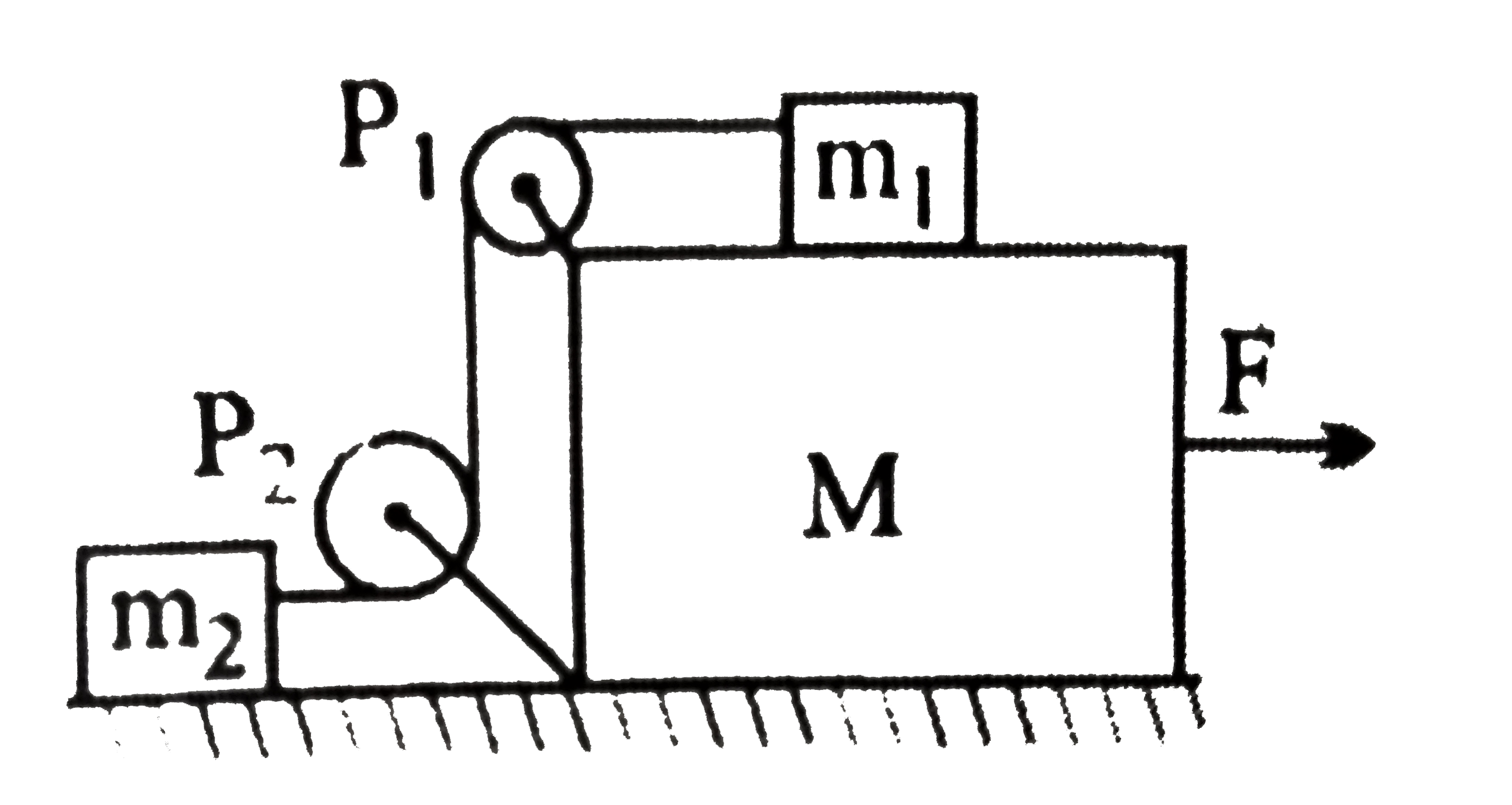
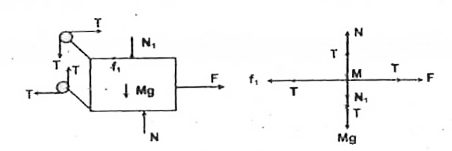
- In the figure masses m(1),m(2) and M are kg. 20 Kg, 5 kg and 50 kg res...
Text Solution
|
- The block each of mass 1 kg are placed as shown .They are connected by...
Text Solution
|
- M(A) = 3 kg ,M(B) = 4 kg ,M(C) = 8 kg. Coefficient of friction between...
Text Solution
|
- Three blocks of masses m(1), m(2) and M are arranged as shown in figur...
Text Solution
|
- In the figure shown m(1)=5 kg,m(2) = 10 kg & friction coefficient betw...
Text Solution
|
- Two masses m(1) kg and m(2) kg passes over an atwoods machine. Find th...
Text Solution
|
- In the figure , masses m(1) , m(2) and M are 20 kg , 5 kg and 50 kg re...
Text Solution
|
- In the figure, pulleys are smooth and strings are massless, m(1)=1 kg ...
Text Solution
|
- In the figure masses m(1),m(2) and M are kg. 5 kg and 50 kg respective...
Text Solution
|