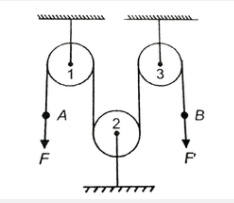
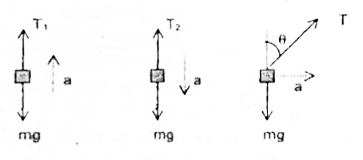
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- The tension at any point of the string AB will be same if
Text Solution
|
- In the given figure mass of string AB is 2kg . Find tension at A,B and...
Text Solution
|
- Three charges +q, +2q and 4q are connected by strings as shown in the ...
Text Solution
|
- Find tension /tensions in the string/strings in the following cases:
Text Solution
|
- The speed of a transverse wave in a stretched string is 348 ms^(-1) , ...
Text Solution
|
- In the following figure, if the tension in the string AB is 51N, then ...
Text Solution
|
- प्रश्न 30 में निम्नतम बिन्दु पर डोरी में तनाव कितना है?
Text Solution
|
- डोरी के एक रइरेसे बंधा हुवे द्रव्यमान m का एक पत्थर ताल में घुमाया जात...
Text Solution
|
- Two identical strings of a stringed musical instrument are in unison w...
Text Solution
|