Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
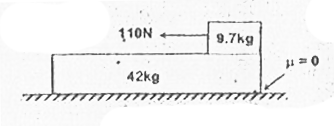
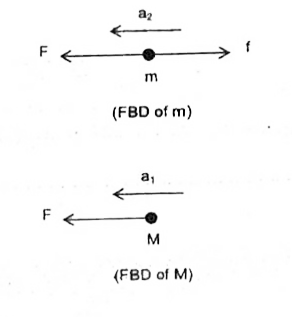
- A 42 kg slab rests on a frictionless floor A 9.7 kg block rests on the...
Text Solution
|
- A 40 kg slb rest on a frictionless floor as shown in the figure. A 10 ...
Text Solution
|
- A 40kg slab rests on a frictionless floor as shown in the figure. A 10...
Text Solution
|
- A slab of 40 kg lying on a frictionales floor and a block of 10 kg res...
Text Solution
|
- A 40 kg slab rests on a frictionless floor . A 10 kg block rests on th...
Text Solution
|
- A 40 kg slab rests on a frictionless floor . A 10 kg block rests on to...
Text Solution
|
- Block A of mass 5 kg is resting on a frictionless floor. Another block...
Text Solution
|
- A 40 kg slab rests on a frictionless floor. A 10 kg block rests on top...
Text Solution
|
- A block of mass 2 kg is placed on the floor. The co-efficient of stati...
Text Solution
|