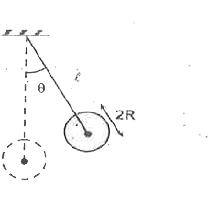
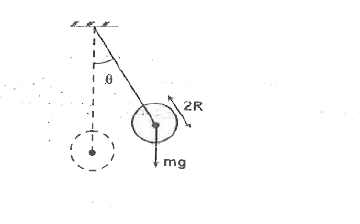
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A spherical bob of mass m and radius R is attached to a fixed point by...
Text Solution
|
- A small bob attached to a light inextensible thread of length l has a ...
Text Solution
|
- Two light strings, each of length l are fixed at points A andB on a fi...
Text Solution
|
- A small bob attached to a light inextensible thread of length l has a ...
Text Solution
|
- A metal wire of length L is suspended vertically from a rigid support....
Text Solution
|
- A compound pendulum consists of a rigid light rod having two spherical...
Text Solution
|
- A small ring of mass m(1) is connected by a string of length l to a sm...
Text Solution
|
- A massless rod rigidly fixed at O. A sting carrying a mass m at one en...
Text Solution
|
- एक दोलक की लंबाई l और इसके बॉब का द्रव्यमान m हैं । यह विरामावस्था मे...
Text Solution
|