Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
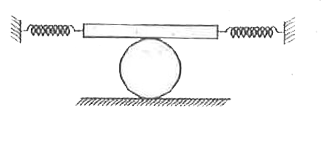
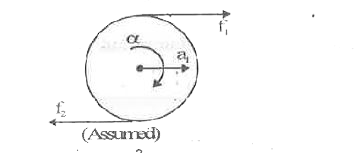
- In the figure shown, mass of the plank is m and that of the solid cyli...
Text Solution
|
- A plank of mass 'm' and area of cross - section A is floating as shown...
Text Solution
|
- A uniform plank of mass m, free to move in the horizontal direction o...
Text Solution
|
- Block A of mass m is placed on a plank B. A light support S is fixed o...
Text Solution
|
- Consider a cylinder of mass M=1 kg and radius R=1 m lying on a rough h...
Text Solution
|
- A uniform plank of mass m = 1kg , free to move in the horizontal direc...
Text Solution
|
- A plank of mass M is placed on a smooth hroizonal surface. Two light i...
Text Solution
|
- A boy pushes a cylinder of mass M with the help of a plank of mass m a...
Text Solution
|
- In the figure shown a plank of mass m is lying at rest on a smooth hor...
Text Solution
|