Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
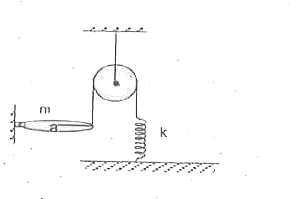
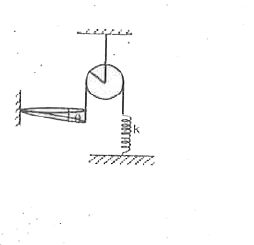
- A ring of mass m and radius a is connected to an inextensible string w...
Text Solution
|
- A light pulley is suspended at the lower end of a spring of constant k...
Text Solution
|
- A ring of mass m is attached to a horizontal spring of spring constant...
Text Solution
|
- A Bead of mass m is attached to one end of a spring of natural length ...
Text Solution
|
- A ring of mass m can slide over a smooth vertical rod. The ring is con...
Text Solution
|
- Four identical spheres having mass M and radius R are fixed tightly wi...
Text Solution
|
- Four identical spheres having mass M and radius R are fixed tightly wi...
Text Solution
|
- A bead of mass m can slide without friction along a vertical ring of r...
Text Solution
|
- One end of a massless spring of spring constant 100 N/m and natural le...
Text Solution
|