Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
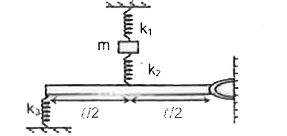
- Find the angular frequency of small oscillation of block m in the arra...
Text Solution
|
- A uniform rod of length 1.00 m is suspended through an end and is set ...
Text Solution
|
- A rigid rod of mass m with a ball of mass M attached to the free end i...
Text Solution
|
- Find the frequency of small oscillations of thin uniform vertical rod ...
Text Solution
|
- In the device shown in Fig, the block m is displaced down slightly and...
Text Solution
|
- A small block is connected to a massless rod, which in turns attached ...
Text Solution
|
- Find the acceleration of the block of mass m. Assume pulleys are massl...
Text Solution
|
- In the arrangements as shown Mgt2m. Find the extension in the spring o...
Text Solution
|
- Uniform rod Ab is hinged at the end A in the figure. The other end of ...
Text Solution
|