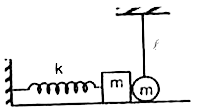
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A pendulum makes perfectly elastic collision with block of m lying on ...
Text Solution
|
- A block of mass 100 g attached to a spring ofstiffness 100 N//Mis lyin...
Text Solution
|
- A simple pendulum of length L has a bob of mass m. The bob is connecte...
Text Solution
|
- Figure shows a system consisting of a massless pulley, a spring of for...
Text Solution
|
- In the figure, the block of mass m, attached to the spring of stiffnes...
Text Solution
|
- A block of mass m is attached to a cart of mass 4m through spring of s...
Text Solution
|
- A block of mass m hangs from three springs having same spring constant...
Text Solution
|
- Three springs of each force constant k are connected as shown figure. ...
Text Solution
|
- A particle of mass m is attached with three springs A,B and C of equal...
Text Solution
|