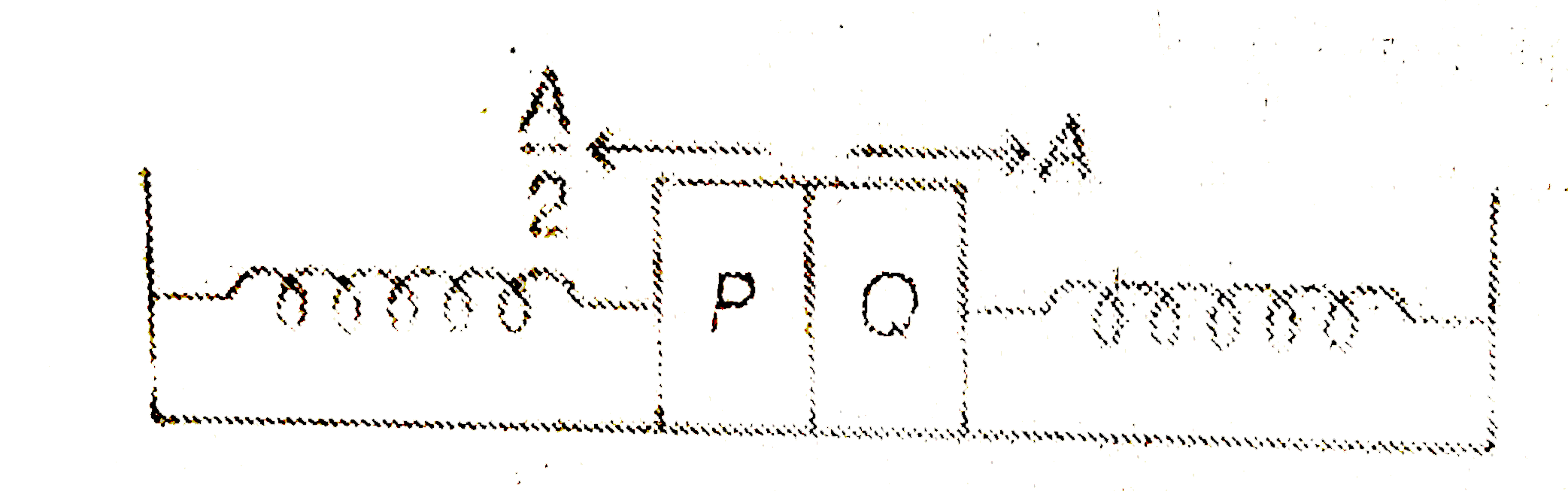A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Passage II) Two identicla blocks P and Q have masses m each. They are ...
Text Solution
|
- A block of mass M is kept on a smooth surface and touches the two spri...
Text Solution
|
- Two identical blocks P and Q have mass m each. They are attached to tw...
Text Solution
|
- Passage II) Two identicla blocks P and Q have masses m each. They are ...
Text Solution
|
- Two identical blocks P and Q have mass m each. They are attached to tw...
Text Solution
|
- Two blocks of masses m(1) and m(2) are kept on a smooth horizontal tab...
Text Solution
|
- Passage II) Two identicla blocks P and Q have masses m each. They are ...
Text Solution
|
- Passage II) Two identicla blocks P and Q have masses m each. They are ...
Text Solution
|
- Passage II) Two identicla blocks P and Q have masses m each. They are ...
Text Solution
|