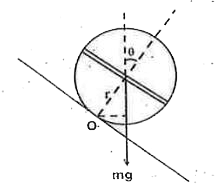
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- In the figure shown a coil of single turns is would on a sphere of ...
Text Solution
|
- In Fig. a coil of single turn is wound on a sphere of radius r and mas...
Text Solution
|
- Figure shows a coil of single turn would on a sphere of radius R and m...
Text Solution
|
- A current of 4A flows through a plane circular coil of radius 4cm havi...
Text Solution
|
- A sphere of mass m and radius r rolls without slipping over a tunnel o...
Text Solution
|
- A current i flows in a circular coil of radius r . If the coil is plac...
Text Solution
|
- A current i flows in a circular coil of radius r. If the coil is place...
Text Solution
|
- Figure shows a larger horizontal coil of radius R carrying a current I...
Text Solution
|
- A coil carrying a current 'I' has radius 'r' and number of turns 'n' i...
Text Solution
|