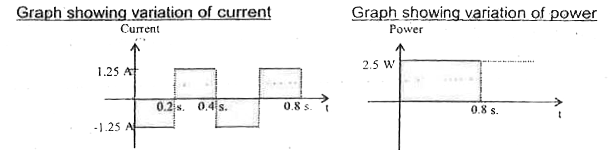
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A thermocol vessel contains 0.5kg of distilled water at 30^(@)C. A me...
Text Solution
|
- A thermocol vessel contains 0.5kg of distilled water at 30^(@)C . A me...
Text Solution
|
- A metal coil of area 5 xx 10^(-3)m^(2), number of turns 100 and resist...
Text Solution
|
- The coil of an a.c. generator has 100 turns, each of cross sectional a...
Text Solution
|
- A current of 5 mA through a coil of 10 turns produces a magnetic field...
Text Solution
|
- एक वृत्ताकार कुंडली 5 xx 10^(-3)T चुंबकीय क्षेत्र में 60^(@) कोण पर रख...
Text Solution
|
- एक थर्मोकोल से बने बर्तन में 0.5 किग्रा आसुत जल 30^(@)C पर भरा है। धा...
Text Solution
|
- The magnetic flux through a coil varies with time t as follows: phi(...
Text Solution
|
- A circular coil of radius 10cm and 25 turns is rotated about its verti...
Text Solution
|