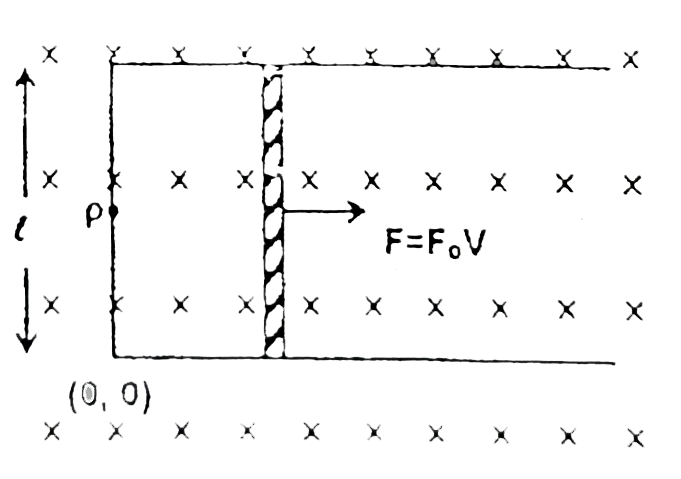
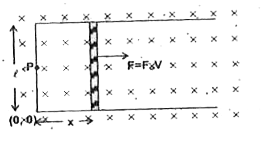
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Two infinite parallel wire, having the cross sectional area 'a' and re...
Text Solution
|
- A straight wire of length l can slide on two parallel plastic rails k...
Text Solution
|
- A wire of length l , mass m and resistance R slides without any fricti...
Text Solution
|
- A conducting wire of length l and mass m can slide without friction on...
Text Solution
|
- Two infinite parallel wire, having the cross sectional area 'a' and re...
Text Solution
|
- A conducting wire of length l and mass m can slide without friction on...
Text Solution
|
- Two metallic wires A and B are connected in parallel. Wire A has lengt...
Text Solution
|
- A long straight wire carries a current I(0), at distance a and b=3a fr...
Text Solution
|
- A long straight wire carries a current I(0). At distance a and b =3a f...
Text Solution
|