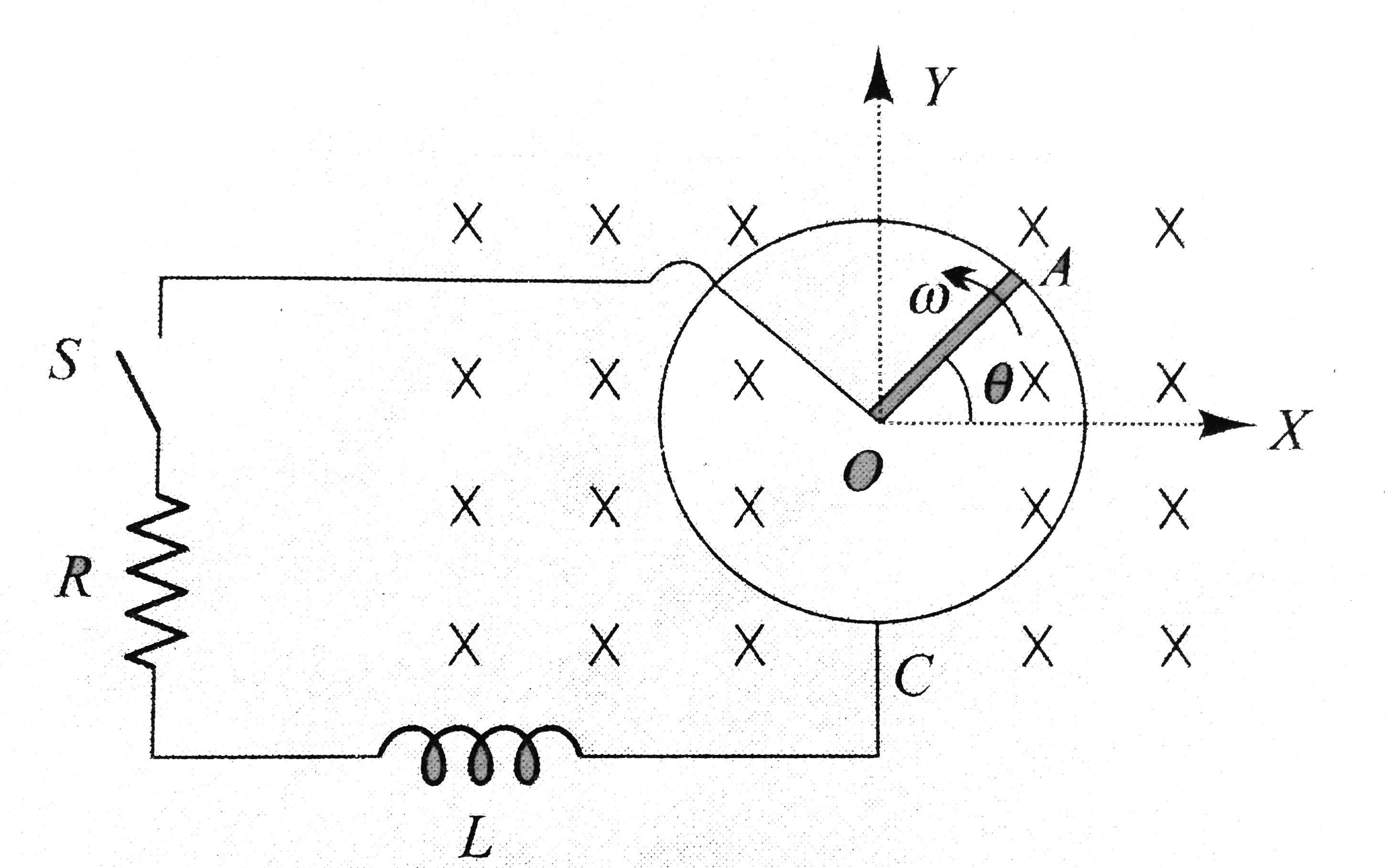Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A metal rod OA of mass m amd length r is kept rotating with a constant...
Text Solution
|
- A metal rod OA of mann 'm' and length 'r' is kept rotating with a cons...
Text Solution
|
- A metal rod of mass m can rotate about a horizontal axis O, sliding...
Text Solution
|
- A uniform rod AB of mass m and length L rotates about a fixed vertical...
Text Solution
|
- A thin circular ring of mass M and radius R is rotating in a horizonta...
Text Solution
|
- A uniform rod of mass m. length L, area of cross- secticn A is rotated...
Text Solution
|
- A rod AB of mass m and length L is rotating in horizontal plane about ...
Text Solution
|
- A long uniform rod of length L, mass M is free to rotate in a horizont...
Text Solution
|
- A circular ring of mass m and radius r is rotating in a horizontal pla...
Text Solution
|