A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
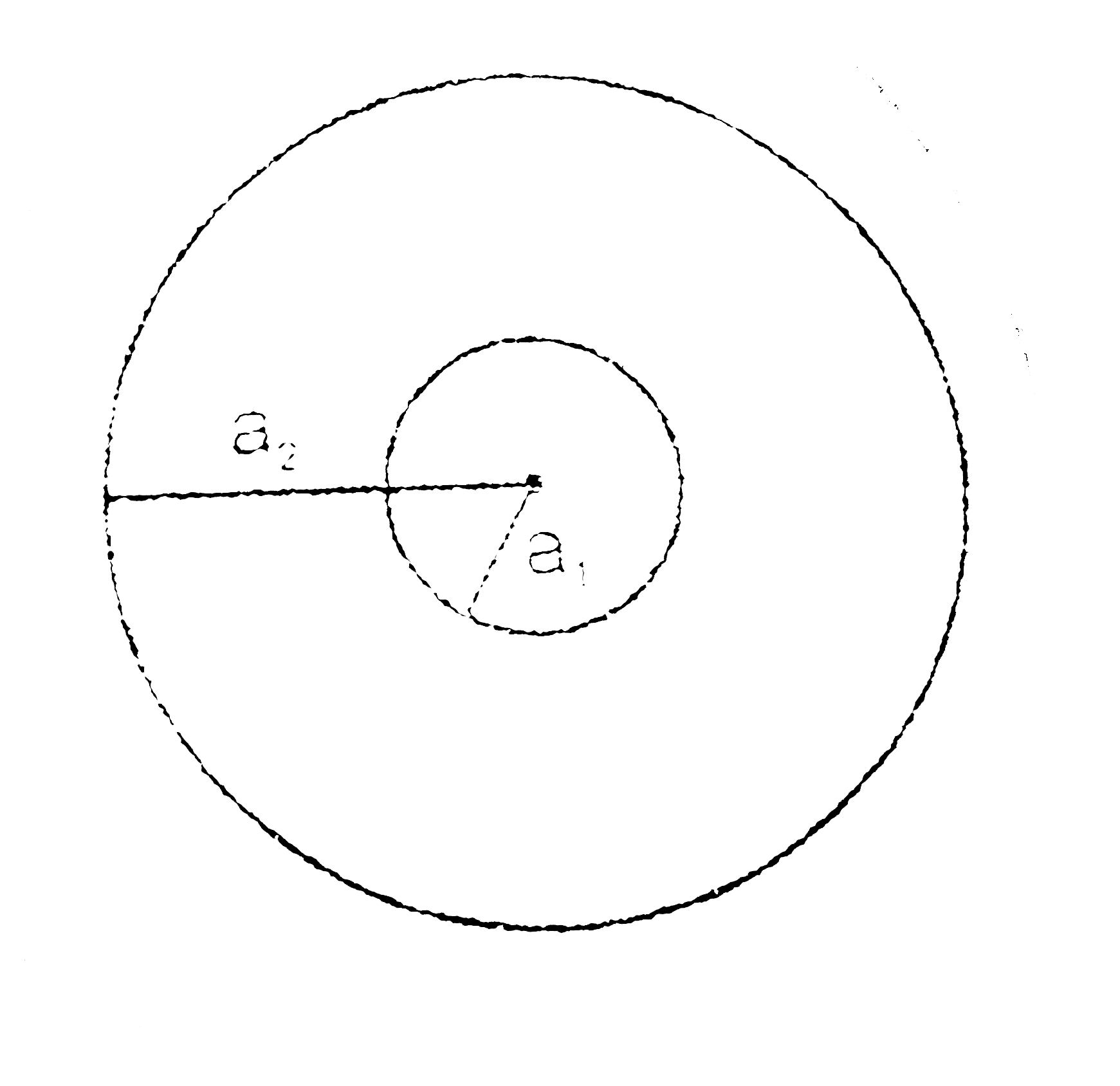
- Find the mutual inductance of two concentric coils of radii a(1) and a...
Text Solution
|
- Find the mutual inductance of two concentric coils of radii a(1) and a...
Text Solution
|
- The number of real roots of the equation 1+a(1)x+a(2)x^(2)+………..a(n)...
Text Solution
|
- Prove that (a(1)^(m)+a(2)^(m)+….+a(n)^(m))/(n)lt((a(1)+a(2)+..+a(n))/(...
Text Solution
|
- If A(j) = ( x-a(j))/( | x- a(j)|) , j = 1,2,"........" n and a(1) lt ...
Text Solution
|
- यदि lt a(n) gt समान्तर श्रेणी में है और a(1)+a(4)+a(7)+.......+a(16...
Text Solution
|
- The number of permutations {a(1),a(2),…,a(10)} of {1,2,3,…,10} satisfy...
Text Solution
|
- The number of real roots of : 1 + a(1)X + a(2) x^(2) .... + a(n) x^...
Text Solution
|
- Prove that a(1)^(m)+a(2)^(m)+….+a(n)^(m)()/(n)lt(a(1)+a(2)+..+a(n))/(n...
Text Solution
|