Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A(1) and A(2) are two ores of metal M.A(1) on calcination gives a blac...
Text Solution
|
- If a1, a2, a3, ,a(2n+1) are in A.P., then (a(2n+1)-a1)/(a(2n+1)+a1)+(...
Text Solution
|
- If a1,a2,a3,...,a(n+1) are in A.P. , then 1/(a1a2)+1/(a2a3)....+1/(ana...
Text Solution
|
- prove that (1)/((a-a(1))^(2)),(1)/(a-a(1)),(1)/(a(1))(1)/((a-a(2))^(2)...
Text Solution
|
- A(1) and A(2) are two ores of metal M.A(1) on calcination gives a blac...
Text Solution
|
- A(1) and A(2) are two ores of metal M. A(1) on calcination gives black...
Text Solution
|
- A(1) " and " A(2) are the two ores of a metal M. They undergo the foll...
Text Solution
|
- a1,a2,a3.....an are in H.P. (a(1))/(a(2)+a(3)+ . . .+a(n)),(a(2))/(a(1...
Text Solution
|
- Let a(1),a(2),a(3), . . .,a(n) be an A.P. Statement -1 : (1)/(a(1)a(...
Text Solution
|
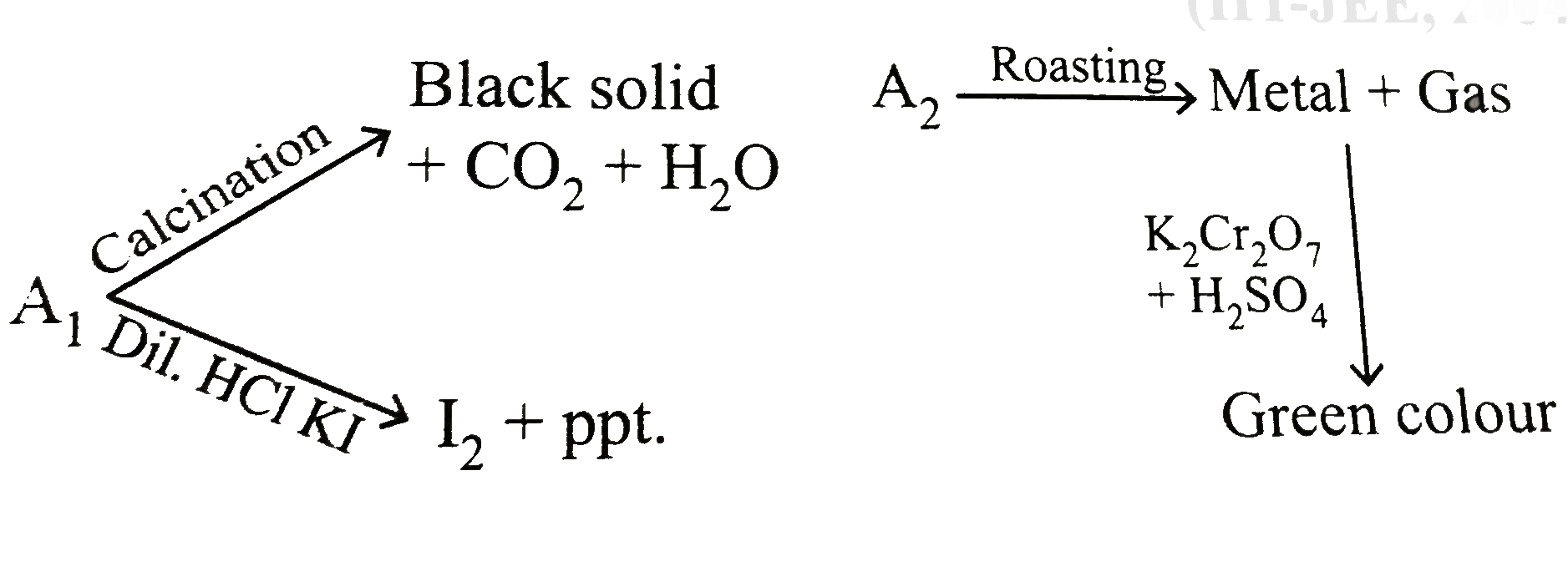 .
.