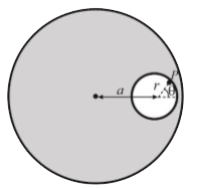
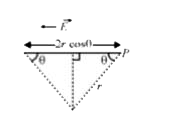
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A solid non-conducting sphere of radius R is charged with a uniform vo...
Text Solution
|
- A cavity of radius r is made inside a solid sphere. The volume charge ...
Text Solution
|
- A cavity of radius r is present inside a fixed solid dielectric sphere...
Text Solution
|
- A cavity of radius r is made inside a solid sphere. The volume charge ...
Text Solution
|
- Inside a uniform sphere of mass M and radius R, a cavity of radius R//...
Text Solution
|
- A Uniformly charged solid non-conducting sphere of uniform volume char...
Text Solution
|
- A cavity of radius r is present inside a solid dielectric sphere of ra...
Text Solution
|
- A solid of radius 'R' is uniformly charged with charge density rho in ...
Text Solution
|
- A solid sphere having radius R and uniform charge density rho has a ca...
Text Solution
|