Topper's Solved these Questions
TRIANGLES
SWAN PUBLICATION|Exercise Other Important Questions (Multiple Choice Questions)|15 VideosTRIANGLES
SWAN PUBLICATION|Exercise Other Important Questions (Fill in the blanks)|8 VideosTRIANGLES
SWAN PUBLICATION|Exercise Exercise 3(Multiple Choice Questions)|7 VideosSYMMETRY
SWAN PUBLICATION|Exercise OTHER IMPORTANT QUESTIONS (Which of the following statement is true and which is false.)|7 VideosVISUALISING SOLID SHAPES
SWAN PUBLICATION|Exercise OTHER IMPORTANT QUESTIONS (III. Which of the following is true and which is false.)|6 Videos
Similar Questions
Explore conceptually related problems
SWAN PUBLICATION-TRIANGLES-Exercise 4
- Which of the following can be the sides of a triangle? 8cm, 10cm, 18...
Text Solution
|
- Which of the following can be the sides of a triangle? 6cm, 4cm, 8cm
Text Solution
|
- Which of the following can be the sides of a triangle? 35cm,38cm, 40...
Text Solution
|
- Which of the following can be the sides of a triangle? 3cm, 4cm, 10c...
Text Solution
|
- A point O is in interior of a DeltaABC use symbols gt, lt or = to make...
Text Solution
|
- A point O is in interior of a DeltaABC use symbols gt, lt or = to make...
Text Solution
|
- A point O is in interior of a DeltaABC use symbols gt, lt or = to make...
Text Solution
|
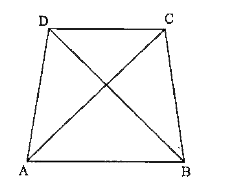
- ABCD is a quadrilateral. Is AB+BC +CD + DA gt AC + BD ?
Text Solution
|
- AD is a median of DeltaABC. Is AB + BC + CA gt 2AD ?
Text Solution
|
- The length of two sies of a triangle are 4cm and 6cm. Between what two...
Text Solution
|