Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NAND LAL PUBLICATION-THE TRIANGLE AND ITS PROPERTIES-Sample Paper for Practice
- Answer the following If PQ= PR in DeltaPQR. Write the pair of equal ...
Text Solution
|
- Answer the following Is it possible to have triangle with the measur...
Text Solution
|
- Answer the following Are the number 6,8,10 form pythagorean triplet ...
Text Solution
|
- Answer the following If one of the exterior angle of a triangle is 1...
Text Solution
|
- In an isosceles triangle the base angles are 15^(@) more than the vert...
Text Solution
|
- One of the exterior angles of a triangle is 100^(@). The interior oppo...
Text Solution
|
- In the adjoining figure PS perpendicular to QR. Also, PR=25cm PS=15cm ...
Text Solution
|
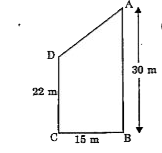
- Two poles 22m and 30m high stand upright on a play ground. If their fe...
Text Solution
|
- In DeltaPQR, angleP=40^(@), PQ||SR, angleSRT=70^(@), then find anglePQ...
Text Solution
|